Seitenverhältnis nach dem goldenen Schnitt online Berechnen:

Goldener Schnitt: Er hilft bei folgenden Fragen:
Was ist harmonisch? Kann man Schönheit definieren oder sogar berechnen? Gibt es eine Gestaltungsregel, die bei der Komposition in der bildenden Kunst hilft?
Fragen, die mit Sicherheit schon jeher kontrovers diskutiert wurden. Denn wie soll man solch ein komplexes Thema in eine Formel packen? Dazu muss es stark vereinfacht werden.
Reduzieren wir dieses Problem auf den Kern, müssen persönliche Vorlieben, kulturelle Einflüsse und ähnliches weggelassen werden. Was bleibt ist die Frage, ob es eine universelle Proportion gibt, die überwiegend als harmonisch wahrgenommen wird.
Ein Weg, sich dieser Herausforderung anzunähern ist der mathematische Weg. Auf der Suche nach einer Antwort müssen wir etwas weiter ausholen:
Der goldene Schnitt – Grundgedanke
Hier wird die Suche nach einer Gesetzmäßigkeit in der Harmonie auf einen Grundgedanken reduziert. Wie kann man eine Strecke zwischen zwei Punkten so teilen, dass die zwei Teilstücke weder langweilig erscheinen, noch eine zu große Spannung aufbauen?
Teilt man die Strecke einfach in der Mitte, entstehen zwei gleich große Stücke. Teilt man die Strecke irgendwo beliebig, stehen die Stücke oft in keinem harmonischem Verhältnis zueinander.
Auf der Suche nach diesem harmonischen Verhältnis kommt jetzt der Goldene Schnitt ins Spiel.
Der Goldene Schnitt, auch als Phi bezeichnet, ist ein Verhältnis, das in der Kunst und Architektur verwendet wird, um Harmonie und Schönheit zu erzeugen. Er beschreibt das Verhältnis zwischen zwei Teilen eines Ganzen, wobei der größere Teil in der gleichen Proportion zum kleineren Teil steht wie der kleinere Teil zum gesamten Ganzen. Dieses Verhältnis wird als “golden” bezeichnet, da es in der Natur häufig vorkommt und als besonders harmonisch empfunden wird.

Wie berechnet man den goldenen Schnitt
Die Strecke B verhält sich zur Strecke A wie A zur Gesamtlänge beider Strecken A+B.
A / B = ( A + B ) / A
bzw.
Die Zahl, die sich aus dieser Berechnung ergibt, wird mit Phi bezeichnet und entspricht in etwa dem gerundeten Wert 1,6180
A / B = φ ≈ 1,6180339887498948
Die Zahl Phi ist ungefähr 1,618 und kommt in der Natur häufig vor. Beispielsweise haben die meisten Schneckenhäuser und viele Blüten eine Form, die dem Goldenen Schnitt entspricht. Auch in der menschlichen Anatomie findet sich dieses Verhältnis, beispielsweise in der Länge von Gliedmaßen im Verhältnis zum Körper.
Wie wird der goldene Schnitt konstruiert?
Konstruktion nach der inneren Teilung
Hier wird eine Strecke so geteilt, dass zwei Teilstrecken im Verhältnis des goldenen Schnittes entstehen:

- Die Strecke S1 in der Hälfte teilen.
- die halbe Strecke am Ende der Strecke im rechten Winkel aufzeichnen (S2).
- die Enden beider Strecken zu einem Dreieck verbinden (S3)
- mit einem Zirkel um den Endpunkt von S2 im Radius der Strecke S2 einen Kreis schlagen
- Der Kreis schneidet Strecke S3
- Um den Anfangspunkt S1 einen Kreis durch den grade erstellten Schnittpunkt durch S3 schlagen.
- Dieser Kreis teilt Strecke S1 in exakt dem Verhältnis des goldenen Schnittes in S1a und S1b
Konstruktion nach der äußeren Teilung
Dabei wir eine Strecke so verlängert, dass die Verlängerung zur Ursprungsstrecke im Verhältnis des Goldenen Schnittes steht:
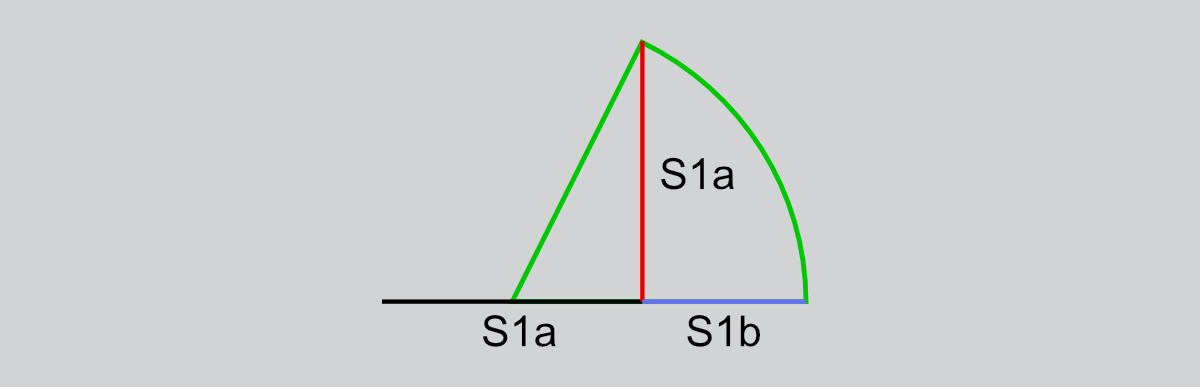
- Am Endpunkt der Strecke S1 Strecke S2 mit der gleichen Länge wie S1 im rechten Winkel zeichnen
- Die Hälfte der Strecke S1 markieren
- Um diesen markierten Punkt einen Kreis schlagen, der durch den Endpunkt der Strecke S2 verläuft.
- Dieser Kreis markiert den Endpunkt der verlängerten Strecke S1 in exakt dem Verhältnis des goldenen Schnittes in S1a und S1b
Wer “erfand” den goldenen Schnitt?
Beobachtet man die Natur, fällt auf, dass viele Dinge harmonischen Proportionen unterliegen. Ein Grund, warum wir die Natur als schön empfinden?
Der Goldene Schnitt wurde bereits von den alten Griechen entdeckt und in der Kunst seitdem weit verbreitet. Er wurde beispielsweise in der Architektur verwendet, um Gebäude und Tempel in harmonischen Proportionen zu errichten. Der berühmte Architekt Le Corbusier verwendete beispielsweise den Goldenen Schnitt in seinen Entwürfen für Gebäude. Auch in der Malerei wurde der Goldene Schnitt verwendet, um Bilder auszugleichen und zu strukturieren. Eines der bekanntesten Beispiele ist die Mona Lisa von Leonardo da Vinci, bei der das Gesicht nach dem Goldenen Schnitt proportioniert ist.
Schon in der Antike wurden die Proportionen des goldenen Schnittes in der Architektur angewandt. Hier geht er auf Euklid (Mathematiker 3. Jahrhundert vor Christus) zurück, der allerdings auf ältere Quellen zurückgegriffen hat (Heron und Ptolemaios)
Die Fibonacci Folge
Im Jahre 1202 veröffentlichte dann Leonardo Fibonacci eine Zahlenfolge, mit der er das Wachstum einer Kaninchenpopulation beschreiben wollte. Es ist eine unendliche folge von Zahlen, bei der jeweils die Summe zweier aufeinanderfolgender Zahlen die jeweils nächste ergibt.
0
1 (0+1)
2 (1+1)
3 (1+2)
5 (2+3)
8 (3+5)
13 (5+8)
…
Je weiter man die Fibonacci Folge fortführt, desto mehr nähert sie sich den Proportionen des goldenen Schnittes an.
Der goldene Schnitt als Strecke, Fläche, Dreieck oder Spirale
Ist die Proportion erst einmal festgelegt, kann man den goldenen Schnitt auf viele geometrische Formen anwenden. Die bekannteste dürfte hier die Spirale einer Nautilus-Muschel sein, deren Aufbau den goldenen Schnitt wiedergibt.
Aber auch die Seiten des Dreieckes lassen sich nach dem goldenen Schnitt aufteilen. Hier wird die Basis als Strecke 1, beide Seiten als Strecke 2 definiert. So können Bilder ebenfalls im Verhältnis des goldenen Schnittes aufgeteilt werden. Man spricht hier vom goldenen Dreieck.
Genauso lassen sich die Proportionen auf Quadrate anwenden.
Anwendung des goldenen Schnittes in der Architektur und Kunst
Proportio Divina („göttliche Proportion“)
In der Fotografie und dem Grafikdesign wird der Goldene Schnitt ebenfalls häufig verwendet, um Aufnahmen und Designs auszugleichen und ansprechender zu gestalten. Beispielsweise kann man bei der Gestaltung von Plakaten oder Flyern den Goldenen Schnitt verwenden, um das Layout auszugleichen und ansprechender zu gestalten.
Fotografie
In der Fotografie wird der Goldene Schnitt ebenfalls verwendet, um Aufnahmen auszugleichen und ansprechender zu gestalten. Beispielsweise könnte man ihn verwenden, um das Verhältnis von Elementen innerhalb einer Aufnahme auszugleichen oder um den Hintergrund im Verhältnis zum Vordergrund auszugleichen.
In vielen Kameras und Bildbearbeitungsprogrammen lassen sich Hilfslinien einblenden. Diese teilen das Bild in 9 gleich große Quadrate, die in ihrem Seitenverhältnis den Proportionen des Goldenen Schnittes entsprechen. Wird das Motiv nun anhand dieser Linien ausgerichtet, entsteht ein dynamischer Bildaufbau.
Malerei
Ebenso wie in der Fotografie lässt sich der Goldene Schnitt in vielen Meisterwerken von der Antike bis zur Moderne erkennen. Leonardo da Vinci – der sich viel mit Mathematik und deren Verhältniss zur Kunst beschäftigt hat – mal als ein hervorstechendes Beispiel genannt. In vielen seiner Bilder lassen sich die Proportionen des Goldenen Schnittes oder goldenen Dreiecks erkennen.
In der Malerei wird der Goldene Schnitt verwendet, um Bilder auszugleichen und zu strukturieren. Beispielsweise könnte man ihn verwenden, um das Verhältnis von Figuren und Objekten innerhalb eines Bildes auszugleichen oder um den Hintergrund im Verhältnis zum Vordergrund auszugleichen. Eines der bekanntesten Beispiele für die Verwendung des Goldenen Schnitts in der Malerei ist die Mona Lisa von Leonardo da Vinci, bei der das Gesicht nach dem Goldenen Schnitt proportioniert ist.
Architektur
Die Architektur ist das Paradebeispiel für die Einsatzfähigkeit des goldenen Schnittes. Kann man diesen schon in antiken Bauten angewandt sehen, erkennt der aufmerksame Beobachter in vielen Gebäuden seine Anwendung. Das ist nicht zuletzt eine Folge der engen Verknüpfung von Mathematik und Architektur.
In der Architektur wird der Goldene Schnitt verwendet, um Gebäude und andere Bauwerke in harmonischen Proportionen zu errichten. Beispielsweise könnte man den Goldenen Schnitt verwenden, um die Höhe eines Gebäudes im Verhältnis zu seiner Breite zu bestimmen oder um die Größe von Fenstern und Türen im Verhältnis zur Wandfläche auszugleichen. Der berühmte Architekt Le Corbusier hat beispielsweise den Goldenen Schnitt in vielen seiner Entwürfe verwendet.
Plastik
Auch in der Plastik – von der Darstellung des menschlichen Körpers, über naturalistische Bildnisse bis zur abstrakten Plastik lässt sich – und wird – der goldene Schnitt gut angewendet.
Grafik Design
Im Grafikdesign wird der Goldene Schnitt auch häufig verwendet, um Layouts auszugleichen und ansprechender zu gestalten. Beispielsweise könnte man ihn verwenden, um das Verhältnis von Text und Bildern innerhalb eines Designs auszugleichen oder um die Größe von verschiedenen Elementen im Verhältnis zueinander auszugleichen.
Ist der goldene Schnitt ein Naturgesetz?
Selbst, wenn er ein Naturgesetz wäre – was würde es ändern?
Es ist ebenfalls in der Natur des Menschen (besonders in der von Künstlern) alles zu hinterfragen und sich gegen Normen aufzulehnen.
Einige werden ihren Bildaufbau streng nach dem goldenen Schnitt ausrichten, einige unbewusst zum gleichen Ergebniss kommen, einige werden sich bewusst dagegen entscheiden – so entsteht die Vielfalt, die wir so schätzen.




